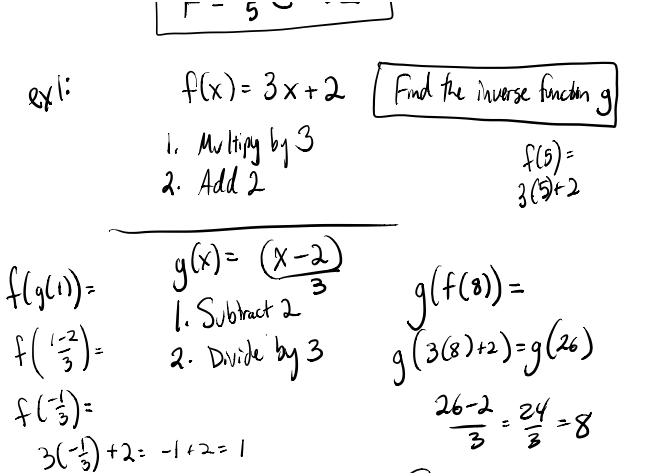Hello all! I made a decision for the rest of this year. I only have so many “writing bucks” that I’m able to spend, and over the past several years most of these have gone towards this blog at the expense of my teaching blog: A Recursive Process. No more. I’m switching over to spend my writing bucks on that blog at the expense of this blog. Follow me there, I should have weekly (ish) posts from here on out. Maybe next year!
105-106 Trig Graphs Desmos Activity
(Calling Photo180 bankruptcy on posts 91-104)
When you find the right desmos activity at the right time with the right class, it’s magical. The conversations that I overheard them having when working through this activity (exploring amplitude and vertical shifts of trig graphs) were just fantastic.


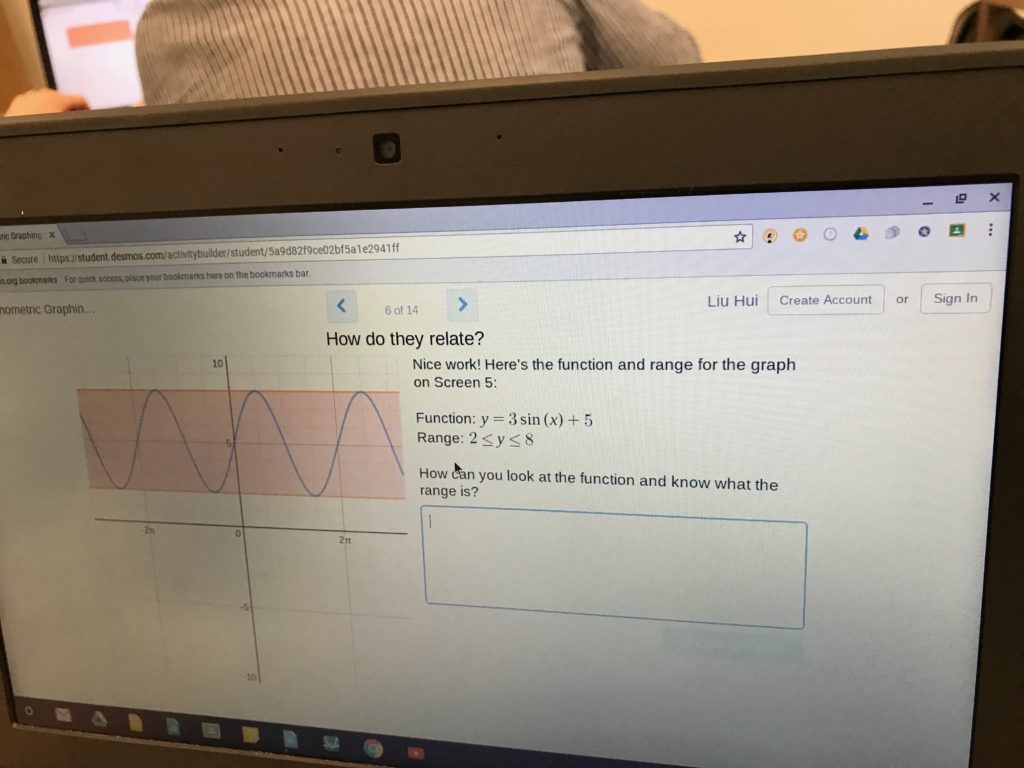
Here’s a student sketching out the maxes and mins of a trig graph so that they could find the amplitude and midline (all terms that they haven’t been introduced to yet) so they could graph y=a*sin(x)+b. 
89-90 Glue Day
From time to time I think my students just need a “glue” day. We’ve learned and practiced a bunch of related skills, but maybe they’ve been somewhat out of context, or they’ve been rushed, or they’ve had a week off of class (ahem Regents), or the learning has been too straightforward. They (and I) appreciate a day to just practice and work together. This happens a lot in our classes, it’s a time for them to bunch together odd learning stuffs into one mass.
Encourage them to work in groups, work how they are comfortable, and I provided a key to the cross-number puzzle that they were working on up front. I walked and answered questions for 40 minutes for each of the 4 sections.
87-88 2nd Quarter Feedback Part 5
Assorted responses to the following prompt:
Anything else you want to say about class to me? Suggestions?
(My responses are in italics)
- it is very hard to do well in this class because i will never need any of this stuff outside of school so there is no motivation to learn here.
Understood. - I do enjoy how laid back this class is, and how comfortable I feel to ask questions. I do not however feel like I am doing well, no matter how hard I study or ask questions. This class, though not difficult, is just confusing and full of quizzes and tests that most times are hard to remember. I understand the need to review as we go along, but it is just too much.
The Algebra 2 curriculum is a bear. I try to make it a less scary bear, but it’s tough. - moving faster so we aren’t spending days on one topic would be beneficial to me
So interesting how most students want me to SLOOOOW down (exact quote), but some say we’re moving too slow. I need to work on better differentiation of the material. - The energy in class makes it go by quickly yet learn a decent amount
- LETS WORK ON Quizes WHEN THEY ARE ASSESSED
This is pushback on the lagged quiz system. I believe in it, but I have to sell it better to some students. - More packets instead of notes.
I’m not a packet teacher, I even tried again this year. I just don’t like what I do and what the students do. I understand that some Teachers can rock that kind of classroom, but not me. Know thy self.

85-86 2nd Quarter Feedback Part 4
Grading System Feedback. Got any?
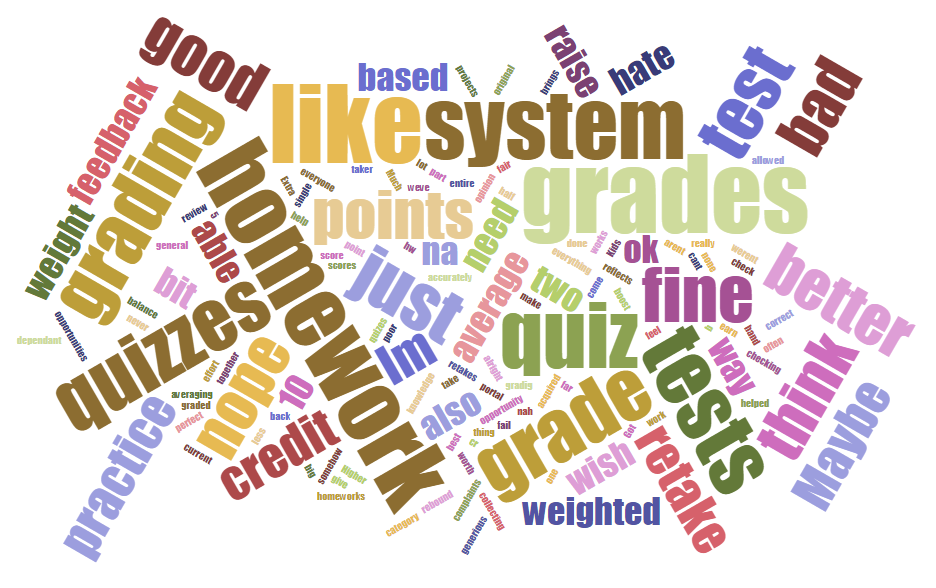
A lot of responses asking for more homework grades to boost the overall grade (this doesn’t make sense as homework is a department required % and wouldn’t matter if I checked it once or 100 times). I’ve explained this many times before. No luck. Sigh. Grade is way too big of a motivator, and it’s been worse this year. Working on it.
83-84 2nd Quarter Feedback Part 3
Prompt:
What can we do to help you learn better in this class?

More practice problems came up a ton. I need to mention that these ~80 responses came from 4 sections of Algebra 2. These students are not in the honors track, nor in the lab track (the lab track has extra time to meet, but they still complete alg2 in one year). It makes sense that they’d want more time for practice, but I don’t know where to find it. We spend an average of less than 10 min per a 40 min period on any version of teacher lead notes. Oh well.
81-82 2nd Quarter Feedback Part 2
The prompt for this word cloud is:
What activities/methods/strategies have we done in class that have NOT worked well for you?

So although whiteboards came up in the first question, it also came up in the methods that aren’t working. Interesting. Notes came up the most, and that makes sense in relation to how we run class through the whiteboards. Many students still want to have a traditional notebook with a class set of notes provided. I allow students to do that, but I don’t actively support it, if they’d like to they can do everything on paper. I think students drastically overestimate how much they would refer to their notes and how helpful that is for them in the long run. There are certainly some students who work best this way, but I think it’s a minority. They also have my classnotes (with all examples and answers) available to them in pdfs on a google drive folder. I don’t think they’re used *that* much anyway.
79-80 2nd Quarter Feedback
Please try a quarter feedback form if you haven’t already. The students provide some great thoughts, and while not all of them are helpful for all; there are so many great things to draw from. Here’s a word cloud to the following question:
What activities/methods/strategies have we done in class that have worked well for you?

Takeaways? Whiteboards. Working in groups. SBG Quiz system.
77-78 Finding Inverses Part 2
(Part 2)


75-76 Finding Inverses
After some FANTASTIC discussion of inverses on twitter (thank you all, you’re the best!), I decided to take the following approach:
- Introduce inverse functions by “undoing” the original function. This has an eventual ending point, as not all functions are easily undone this way (f(x) = (x+1)/(x-2) for example).
- After much practice, then build in the “switch x and y” and solve for y method.
Hopefully their thought pathways for inverses are built up enough so that the procedure change doesn’t mess up the previous understanding.